Compression des données de graphes : du traitement du signal à l'apprentissage automatique

Le traitement des signaux de graphes (GSP) [1-3] et l'apprentissage automatique des graphes (GML) [4-6] sont des domaines de recherche qui visent à généraliser les concepts classiques du traitement des signaux et de l'apprentissage automatique aux données définies sur des graphes. Dans le GSP, les opérations classiques telles que le filtrage, l'échantillonnage et la reconstruction sont étendues aux signaux de graphes, c'est-à-dire aux fonctions définies sur les sommets d'un graphe [7,8]. Dans le GML, les architectures de réseaux neuronaux sont adaptées aux données structurées en graphes, ce qui conduit à des modèles tels que les réseaux neuronaux à base de graphes (GNN) [9] et les réseaux neuronaux à passage de messages (MPNN) [10]. Le GSP et le GML sont essentiels car les données structurées en graphes apparaissent dans de nombreuses applications, notamment les réseaux sociaux [3], le web [11], les systèmes de recommandation [12], les réseaux biologiques [13] et les graphes de connaissances [14], entre autres. Un défi commun à tous ces domaines est l'échelle massive des graphes sous-jacents, qui contiennent souvent des millions, voire des milliards de nœuds et d'arêtes [15]. Il devient donc essentiel de compresser les signaux qui y sont définis, ce qui permet également un apprentissage et un traitement efficaces des représentations compressées.

Dans la littérature sur le GSP, de nombreux travaux ont abordé les problèmes d'échantillonnage et de reconstruction des signaux de graphes de manière systématique [7,16-18]. Ces travaux fournissent des garanties théoriques pour la reconstruction des signaux de graphes à partir d'échantillons basés sur les propriétés spectrales du graphe, guidant la conception d'ensembles d'échantillonnage optimaux ou quasi optimaux [8,19,20]. Cependant, ces méthodes supposent que le graphe d'origine n'est pas modifié et ne prennent en compte que le problème de l'échantillonnage des signaux de graphes. En parallèle, la communauté GML a développé des méthodes de grossissement de graphes fondées sur des principes [21] et, plus récemment, des techniques de grossissement de graphes avec des garanties de transmission de messages [22,23]. Cependant, les opérateurs de réduction/élévation et de propagation associés sont difficiles à optimiser dans la pratique, ce qui limite leur évolutivité.

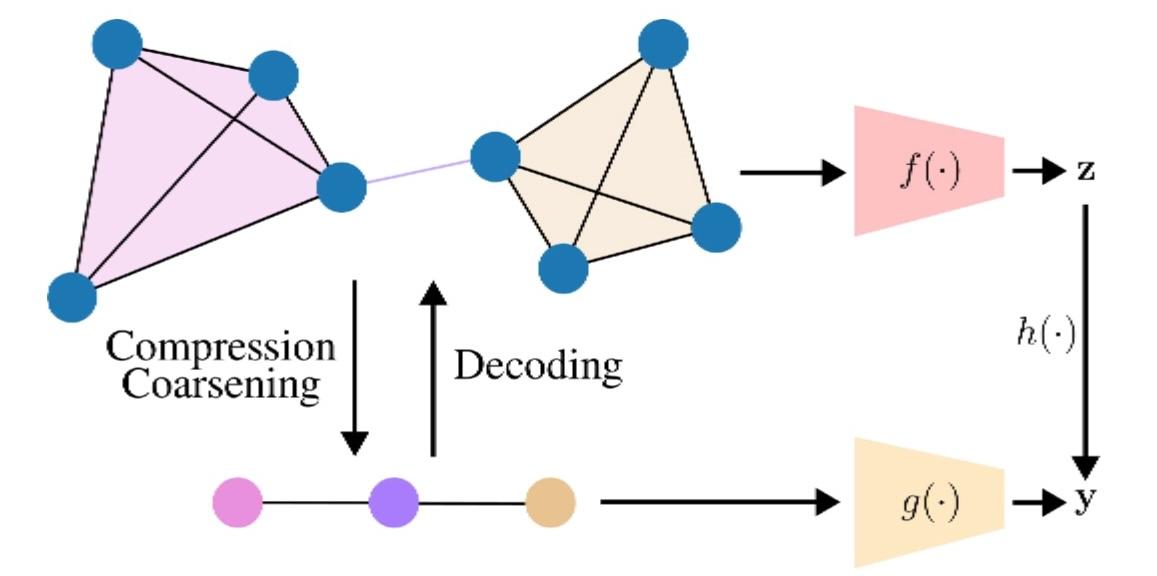
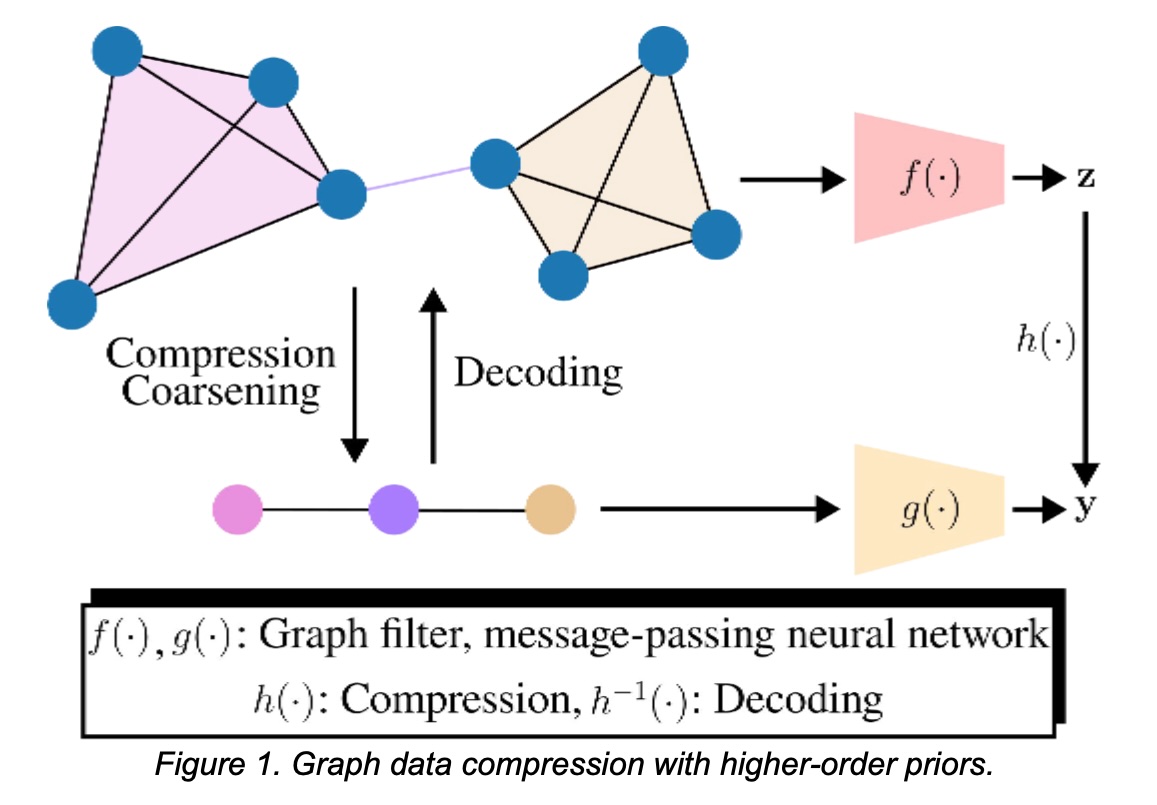
La mise en place d'un cadre fondé sur des principes pour compresser conjointement les signaux de graphes et la topologie avec (i) des garanties de décodage et (ii) des garanties au niveau des tâches sur la topologie compressée reste un défi à relever. Nous abordons cette question en supposant l'accès à des structures d'ordre supérieur (par exemple, des cliques/motifs) qui induisent un opérateur d'agrégation et un graphe compact, comme le montre la figure 1. Cette priorité nous permettra (i) de compresser les signaux et de les décoder avec certaines garanties, et (ii) d'exécuter des GNN directement sur la représentation compressée tout en préservant les performances en aval. Contrairement aux agrégations locales successives [18], qui forment des mesures en appliquant de manière répétée une fonction de décalage de graphe tout en conservant la topologie, nous supposons une priorité d'ordre supérieur, comme les cliques, qui induit l'opérateur de compression et une topologie compressée sur laquelle l'apprentissage se poursuit. De même, contrairement à la méthode de grossissement de graphes avec garanties de passage de messages qui construit des opérateurs de réduction/élévation [22,23], notre a priori d'ordre supérieur fournit la carte d'agrégation, simplifiant la conception des opérateurs tout en permettant des garanties pour la propagation GNN/MPNN. Une question clé que nous étudions est la suivante : quand ces a priori d'ordre supérieur sont-ils informatifs et utiles dans la pratique ? Nous ciblons les régimes où les cliques/motifs sont courants (par exemple, les sous-structures de type communautaire), afin que l'agrégation capture les variations douces dans la clique/le motif et préserve les performances de la tâche. Ce problème a de nombreuses applications, allant de la compression et du stockage de données de graphes au traitement efficace d'ensembles de données relationnelles dans des domaines tels que les réseaux sociaux, le web, les systèmes de recommandation et les systèmes biologiques.